Poker Odds & Outs: The Simple Guide
Share
In our poker math and probability lesson it was stated that when it comes to poker; “the math is essential“. While you don’t need to be a math whiz to succeed at poker, a strong grasp of probability is a game-changer—because poker is all about understanding the odds. As the saying goes, there are good bets and bad bets, and poker reveals who knows the difference. That insight speaks to how crucial poker math really is.
In this lesson, we break down drawing odds in poker and how to assess your chances of landing a winning hand. We’ll start with essential poker math and guide you step-by-step through the correct way to calculate your odds. Don’t worry about complex equations—we’ll simplify everything and share easy shortcuts so you can make fast, confident plays at the table.
Basic Math – Odds and Equity
In poker (and other probability-based games), equity is your share of the pot based on your current chance to win. If you have a 25% chance of winning, you have 25% equity in the pot.
Odds can be expressed “for” or “against” an outcome. For example, if you hold four cards to a flush with one card to come, the odds against completing the flush are about 4-to-1. That’s a ratio, not a fraction—it doesn’t mean “one-quarter.”
To convert to odds for, add the two numbers: 4 + 1 = 5. So you’ll hit your flush once in every 5 tries. In equity terms, that’s 20% (100 ÷ 5).
Here are some examples:
- 2-to-1 against = 1 out of every 3 times = 33.3%
- 3-to-1 against = 1 out of every 4 times = 25%
- 4-to-1 against = 1 out of every 5 times= 20%
- 5-to-1 against = 1 out of every 6 times = 16.6%
Converting odds into a percentage:
- 3-to-1 odds: 3 + 1 = 4. Then 100 / 4 = 25%
- 4-to-1 odds: 4 + 1 = 5. Then 100 / 5 = 20%
Converting a percentage into odds:
- 25%: 100 / 25 = 4. Then 4 – 1 = 3, giving 3-to-1 odds.
- 20%: 100 / 20 = 5. Then 5 – 1 = 4, giving 4-to-1 odds.
Another method of converting percentage into odds is to divide the percentage chance when you don’t hit by the percentage when you do hit. For example, with a 20% chance of hitting (such as in a flush draw) we would do the following; 80% / 20% = 4, thus 4-to-1. Here are some other examples:
- 25% chance = 75 / 25 = 3 (thus, 3-to-1 odds).
- 30% chance = 70 / 30 = 2.33 (thus, 2.33-to-1 odds).
Some people are more comfortable working with equity rather than odds, and vice versa. What’s most important is that you fully understand how odds work, because now we’re going to apply this knowledge of odds to the game of poker.
Counting Your Outs
Before calculating poker odds, you must first identify your “outs.” An out is any card that improves your hand. For instance, on a flush draw with four hearts, nine hearts remain in the deck to complete the flush. Since each suit has 13 cards, the math is simple: 13 minus 4 equals 9.
For very large draws (13+ outs), this method slightly overestimates your chances by a few percentage points. However, for typical draws (12 or fewer outs), it remains highly accurate and reliable in practice.
Another example would be if you hold a hand like 
and hit two pair on the flop of 
. You might already have the best hand, but there’s room for improvement and you have four ways of making a full house. Any of the following cards will help improve your hand to a full house; 
.
The following table provides a short list of some common outs for post-flop play. I recommend you commit these outs to memory:
Table #1 – Outs to Improve Your Hand
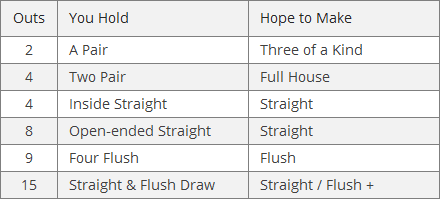
The next table provides a list of even more types of draws and give examples, including the specific outs needed to make your hand. Take a moment to study these examples:
Table #2 – Examples of Drawing Hands (click to enlarge)
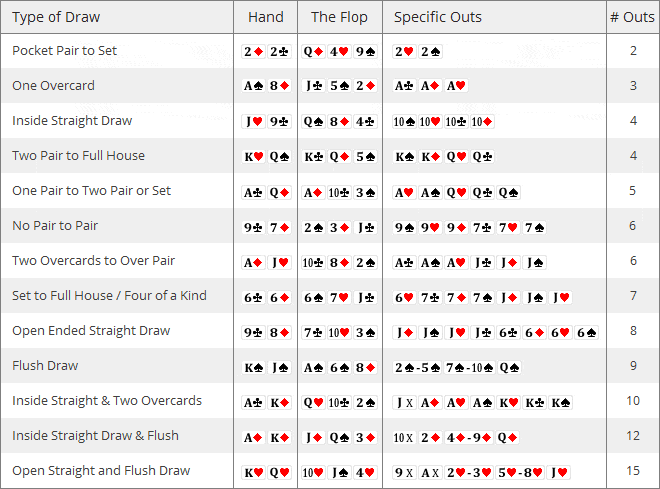
Counting outs is a fairly straightforward process. You simply count the number of unknown cards that will improve your hand, right? Wait… there are one or two things you need to consider:
Don’t Count Outs Twice
There are 15 outs when you have both a straight and flush draw. You might be wondering why it’s 15 outs and not 17 outs, since there are 8 outs to make a straight and 9 outs for a flush (and 8 + 9 = 17). The reason is simple… in our example from table #2 the and the 
will make a flush and also complete a straight. These outs cannot be counted twice, so our total outs for this type of draw is 15 and not 17.
Anti-Outs
There are outs that will improve your hand but won’t help you win. For example, suppose you hold 
on a flop of 
. You’re drawing to a straight and any two or any seven will help you make it. However, the flop also contains two hearts, so if you hit the 
or the you will have a straight, but could be losing to a flush. So from 8 possible outs you really only have 6 good outs.
It’s generally better to err on the side of caution when assessing your possible outs. Don’t fall into the trap of assuming that all your outs will help you. Some won’t, and they should be discounted from the equation. There are good outs, no-so good outs, and anti-outs. Keep this in mind.
Calculating Your Poker Odds
Once you’ve identified your outs—only counting the “clean” or reliable ones—it’s time to calculate your odds. There are several ways to determine your chances of hitting those outs, and we’ll cover three effective methods. The first approach requires no math at all—just refer to the convenient chart provided below.
Table #3 – Poker Odds Chart
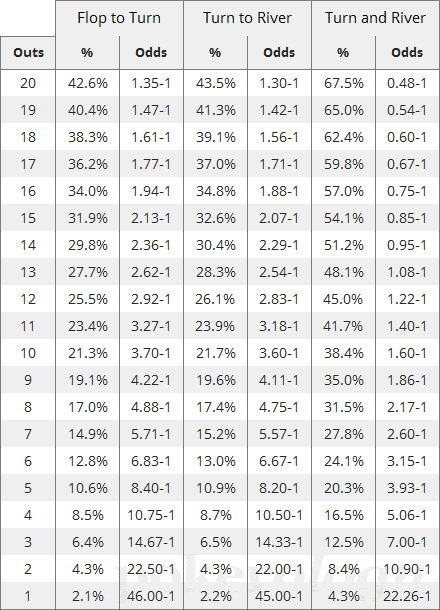
As you can see in the above table, if you’re holding a flush draw after the flop (9 outs) you have a 19.1% chance of hitting it on the turn or expressed in odds, you’re 4.22-to-1 against. The odds are slightly better from the turn to the river, and much better when you have both cards still to come. Indeed, with both the turn and river you have a 35% chance of making your flush, or 1.86-to-1.
We have created a printable version of the poker drawing odds chart which will load as a PDF document (in a new window). You’ll need to have Adobe Acrobat on your computer to be able to view the PDF, but this is installed on most computers by default. We recommend you print the chart and use it as a source of reference. It should come in very handy.
Doing the Math – Crunching Numbers
There are a couple of ways to do the math. One is complete and totally accurate and the other, a short cut which is close enough.
Let’s again use a flush draw as an example. The odds against hitting your flush from the flop to the river is 1.86-to-1. How do we get to this number? Let’s take a look…
With 9 hearts remaining there would be 36 combinations of getting 2 hearts and making your flush with 5 hearts. This is calculated as follows:
(9 x 8 / 2 x 1) = (72 / 2) ≈ 36.
This is the probability of 2 running hearts when you only need 1 but this has to be figured. Of the 47 unknown remaining cards, 38 of them can combine with any of the 9 remaining hearts:
9 x 38 ≈ 342.
Now we know there are 342 combinations of any non heart/heart combination. So we then add the two combinations that can make you your flush:
36 + 342 ≈ 380.
The total number of turn and river combos is 1081 which is calculated as follows:
(47 x 46 / 2 x 1) = (2162 / 2) ≈ 1081.
Now you take the 380 possible ways to make it and divide by the 1081 total possible outcomes:
380 / 1081 = 35.18518%
This number can be rounded to .352 or just .35 in decimal terms. You divide .35 into its reciprocal of .65:
0.65 / 0.35 = 1.8571428
And voila, this is how we reach 1.86. If that made you dizzy, here is the short hand method because you do not need to know it to 7 decimal points.
The Rule of Four and Two
A much easier way to estimate poker odds is the Rule of 4 and 2. When you’ll see both the turn and river, multiply your outs by 4. When there’s only one card to come, multiply your outs by 2 instead.
For example, if a player goes all-in and your call guarantees you’ll see both remaining cards, a flush draw with 9 outs is roughly 9 × 4 = 36%. It won’t match the exact chart percentage, but it’s close enough to guide a solid decision.
With one card to come, it’s even simpler. That same flush draw is about 9 × 2 = 18%. An 8-out straight draw works the same way: 8 × 2 = 16%, which is very close to the true 17%. It’s quick, practical, and easy to apply at the table—no advanced math required.
Conclusion
In this lesson we’ve covered a lot of ground. We haven’t mentioned the topic of pot odds yet – which is when we calculate whether or not it’s correct to call a bet based on the odds. This lesson was step one of the process, and in our pot odds lesson we’ll give some examples of how the knowledge of poker odds is applied to making crucial decisions at the poker table.
When calculating poker odds, rely on charts—these numbers are tested, and the math is solid. Memorize common drawing scenarios, such as a flush draw giving nearly 4-to-1 odds, or around a 20% chance of hitting. Mastering these figures streamlines pot odds calculations, saving effort and focus—something we’ll explore further in the next lesson.
